Validation: Wavelength
| Introduction |
| LSF Reference Data |
| Building LSFPARMS |
| Caveats |
| Validation |
| Summary |
| Other Links |
| isis |
| mit/cxc |
| ciao |
| caldb |
Wavelength
As mentioned earlier, we utilize four generic functions (2 Gaussians and 2 Lorentzians) to parameterize a line profile. The position of each function generally follows the trend described by the grating equation,
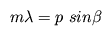
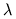 is the photon
wavelength in angstroms, p is the spatial period of the grating lines,
and
is the photon
wavelength in angstroms, p is the spatial period of the grating lines,
and 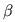 is the dispersion angle. However, small deviation from the
grating relation may occur, as we freely manipulate the four functions to describe
line profiles at any wavelengths. Hypothetically speaking it is plausible that
the dominant Gaussian component may be shifted off-center slightly and then compensate
the shift by altering both amplitude and position of one (or 2) of Lorentzian
components, or vice versa. Hence we need an additional higher order polynomial
fit to compensate such fluctuation.
is the dispersion angle. However, small deviation from the
grating relation may occur, as we freely manipulate the four functions to describe
line profiles at any wavelengths. Hypothetically speaking it is plausible that
the dominant Gaussian component may be shifted off-center slightly and then compensate
the shift by altering both amplitude and position of one (or 2) of Lorentzian
components, or vice versa. Hence we need an additional higher order polynomial
fit to compensate such fluctuation.
For each of the four functions, the centroid position is derived in the dispersion angle (in radian). At a very small angle, the dispersion angle is proportional to the wavelength value. So we fit a linear function to the angle-vs.-wavelength trend and then derive the scale of deviation of data points from the linear trend. The deviation points are fitted with piece-wise quadratic functions in order to ensure continuity on position and slope at each junction defined by the measured data points (see Figures 7 and 8 for the results of the fitting). Then later this non-linear term is added to the linear function to complete the analysis.
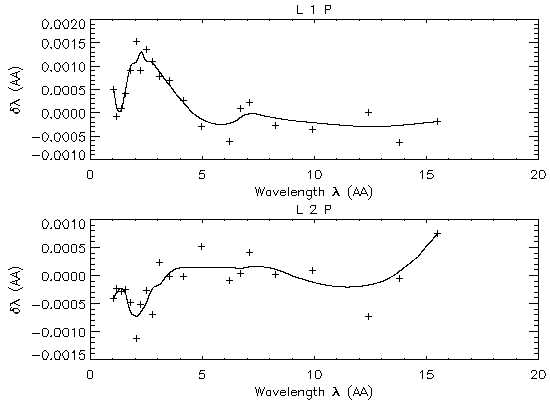
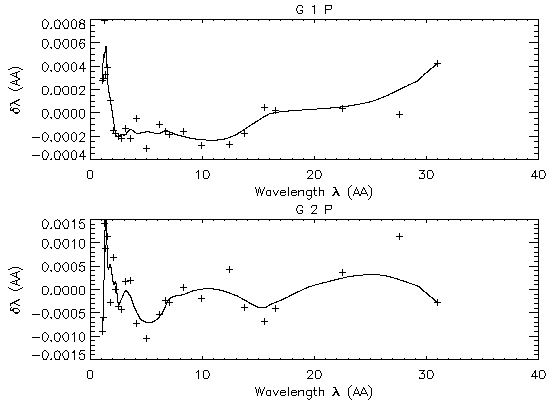
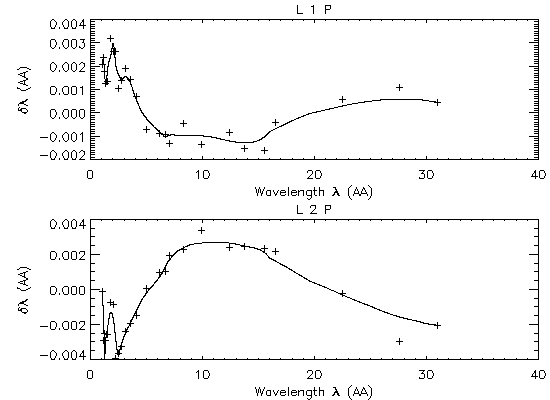
This step in the processing also minimizes any significant non-linearity in the wavelength/dispersion scale resulting from the instrumental design. Both HRC-S and ACIS-S, for example, form their detector surfaces by ajoining 3 to 6 planer-surface detectors (MCPs or CCDs), i.e., not precisely a Rowland torus (but mimicking closely by design). This type of non-linearity can be implicitly taken out with our new procedure.
Line Profile: Wavelength
Once again we run a number of mono-energetic marx simulations and analyze the line spectra by fitting a delta function with isis. The measured line centroid positions are then compared with the expected values to see the difference. Figures 9 and 10 illustrate the difference (Expected - Measured).
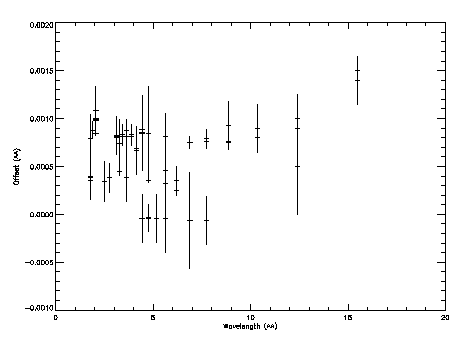
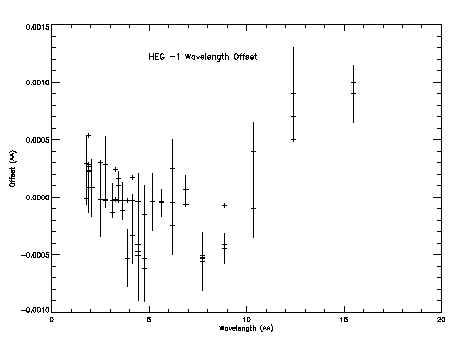
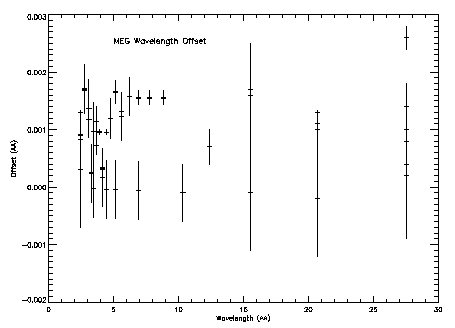
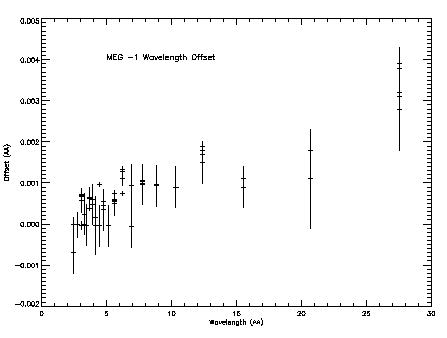
Note that the measured offsets are below the defined instrumental accuracy of HEG or MEG.
Addetum: J. Drake and D. P. Huenemoerder et al. inform me that the growing trend in offset seen in Figures 9 and 10 may be real and primarily due to some coding bug introduced within CIAO. The same effect is more noticeable in LETG/HRC-S (which would seriously affect users' scientific analysis with LETG/HRC-S).
| Previous: Validation: Flux Estimate | Next: Validation: Real HETG dataset |