[Last Change: 28 Feb 2011 (rev 4)]
HRMA On-orbit Focal Length
Ping Zhao, Smithsonian Astrophysical Observatory
August 8, 2000
Definitions
For a point source of infinite distance with a small offaxis angle, θ, its image is projected to the focal plane (a flat plane perpendicular to and intersect with the optical axis at the on-axis focus) at a distance
r from the onaxis focus. The HRMA On-orbit Focal Length (FL) is defined as:
FL = r/tan(θ)
The designed HRMA On-orbit Focal Length (for an ideal HRMA) is:
FL(ideal) = 10065.54532 mm
Estimates based on on-ground measurements
For the real HRMA, there was no direct measurement of its On-orbit Focal Length possible before launch. However, there were six different estimates of the absolute distance between the HRMA On-orbit focus to the front surface (paraboloid side) of the Central Aperture Plate (CAP Datum A), based on several independent direct measurements during various stages of the Chandra development. They are:
| Source of estimate |
HRMA focus to Datum A (mm) |
| Kodak from ATP & ARM data 1 |
10079.5 |
| SAO from ATP & ARM data 2 |
10079.4 |
| TRW from XRCF data (measurement 1) 3 |
10079.1 |
| TRW from XRCF data (measurement 2) 3 |
10080.2 |
| TRW from FACT data (measurement 1) 4 |
10081.9 |
| TRW from FACT data (measurement 2) 4 |
10079.5 |
| Average |
10079.93 |
| Standard Deviation |
1.03 |
- ATP & ARM
- HRMA Acceptance Test Procedure & Factory Alignment Reference Mirror.
- XRCF
- Cross check using the laser rangefinder done at the XRCF.
- FACT
- Focus Alignment Cross-Check done at the observatory level at TRW.
References:
- Email from Atkinson/Kodak dated 12 Aug 1997.
- Memo by Podgorski & Gaetz/SAO dated 29 Aug 1997.
- Email from Texter/TRW dated 17 Apr 1997.
- Email from Podgorski/SAO dated 10 Feb 1998.
This gives a good estimate of the absolute distance between the HRMA focus to the CAP Datum A, and a good estimate of the uncertainty, which is about one millimeter.
SAOSAC Raytrace Calculation
Meantime, SAOSAC
raytrace (with focus turned on, hence the scattering is turned off) gives the distance between the HRMA focus to the CAP Datum A to be 10079.772 mm, which differs only 0.17 mm from the average of the above measurements and well within the measurement errors. This is very important since the SAOSAC is build around the HRMA model based on the HDOS metrology, Kodak assembly and the XRCF X-ray test data; and it is completely independent of the above absolute measurements of the HRMA focus to Datum A distance. This indicates that the current HRMA model in SAOSAC is a faithful representation of the real HRMA regarding the focal length.
Therefore the HRMA On-orbit Focal Length can be calculated with good faith using the SAOSAC. The following fingure illustrates the method of this calculation. Rays from onaxis source come in parallel to the HRMA optical axis and are focused at the onaxis focal point F. The Focal Plane is a flat plane intersect with the optical axis at F. (Detector HRC-I is placed in this plane.) Rays from a offaxis source come in with a small angle theta from the optical axis and are focused on a curved surface between the Focal Plane and the HRMA. The HRMA Focal Length is the distance between points O and F on the optical axis. However, the position of O is unknown. In SAOSAC, the Z-axis is the optical axis and the CAP Datum A is at Z = 0.

For onaxis and offaxis sources, SAOSAC calculates coordinates of the best focal positions as (xo,yo,zo) and (x,y,z) (see Figure 1).
Let r' = sqrt[ (x-xo)2 + (y-yo)2 ]
FL = r' / tan(θ) + zo - z
This way the FL can be calculated using SAOSAC, for different energies and offaxis angles.
Results
The following plots show the results of these calculations for
- Energy
- 0.277 keV, 1.497 keV, 4.511 keV, 6.404 keV, 8.639 keV, and 9.00 keV
- Offaxis angles
- 1', 2', 3', 5', 7', 10', 15', 20'
- Azimuthal angles
- 0°, 90°, 180°, 270°
To summarize, (The dotted line in the figure is the designed HRMA Focal Length and Plate Scale.
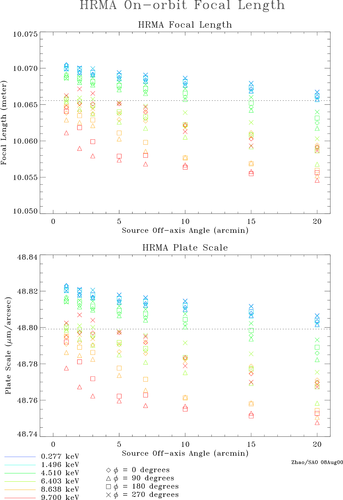
It is seen that the HRMA FL is a function of energy and offaxis angle. And it is also slightly asymmetric azimuthally.
The following table shows the HRMA On-orbit Focal Length averaged for each energy within certain radii of offaxis angles.
Average HRMA On-orbit Focal Length (mm)
| Energy |
Offaxis angle within radius of (arcmin) |
| (keV) |
3 |
5 |
10 |
15 |
20 |
| 0.2770 |
10069.782 ± 0.463 |
10069.571 ± 0.571 |
10069.164 ± 0.787 |
10068.902 ± 0.988 |
10068.563 ± 1.303 |
| 1.4967 |
10069.737 ± 0.463 |
10069.524 ± 0.573 |
10069.116 ± 0.790 |
10068.852 ± 0.994 |
10068.509 ± 1.313 |
| 4.5108 |
10068.465 ± 0.470 |
10068.228 ± 0.621 |
10067.723 ± 0.957 |
10067.336 ± 1.334 |
10066.773 ± 1.982 |
| 6.4038 |
10065.213 ± 0.688 |
10064.884 ± 0.965 |
10064.154 ± 1.506 |
10063.685 ± 1.874 |
10063.064 ± 2.460 |
| 8.6389 |
10063.697 ± 0.938 |
10063.280 ± 1.318 |
10062.373 ± 2.162 |
10061.872 ± 2.472 |
10061.308 ± 2.837 |
| 9.7000 |
10063.219 ± 3.145 |
10062.760 ± 3.419 |
10061.841 ± 3.600 |
10061.253 ± 3.722 |
10060.722 ± 3.820 |
| |
| Mean |
10066.685 ± 3.079 |
10066.374 ± 3.254 |
10065.728 ± 3.601 |
10065.316 ± 3.813 |
10064.823 ± 4.063 |
For a near axis (θ ≤ 3 arcmin) soft source (E < 2 keV), the HRMA Focal Length = 10069.760 ± 0.454 mm. Considering the systematic error of 1mm from the direct on-ground measurements. We have:
HRMA On-orbit Focal Length = 10069.8 ± 1.1 mm
HRMA Near Axis Plate Scale = 48.8196 ± 0.0053 μ/arcsec
 For onaxis and offaxis sources, SAOSAC calculates coordinates of the best focal positions as (xo,yo,zo) and (x,y,z) (see Figure 1).
For onaxis and offaxis sources, SAOSAC calculates coordinates of the best focal positions as (xo,yo,zo) and (x,y,z) (see Figure 1).
 It is seen that the HRMA FL is a function of energy and offaxis angle. And it is also slightly asymmetric azimuthally.
The following table shows the HRMA On-orbit Focal Length averaged for each energy within certain radii of offaxis angles.
It is seen that the HRMA FL is a function of energy and offaxis angle. And it is also slightly asymmetric azimuthally.
The following table shows the HRMA On-orbit Focal Length averaged for each energy within certain radii of offaxis angles.
 For onaxis and offaxis sources, SAOSAC calculates coordinates of the best focal positions as (xo,yo,zo) and (x,y,z) (see Figure 1).
For onaxis and offaxis sources, SAOSAC calculates coordinates of the best focal positions as (xo,yo,zo) and (x,y,z) (see Figure 1).
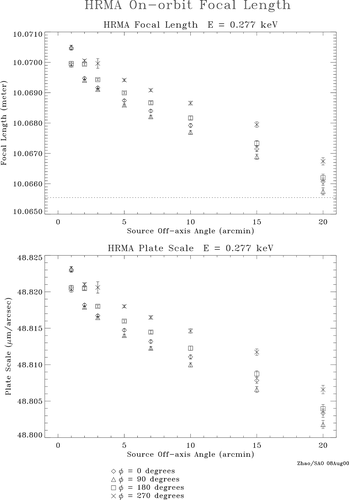
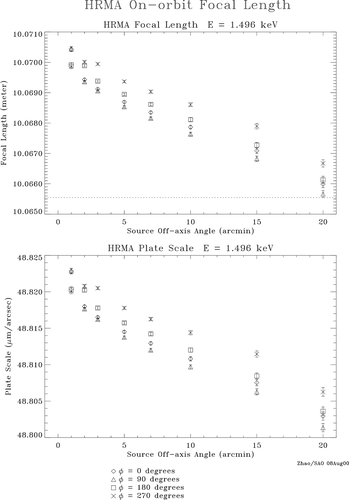
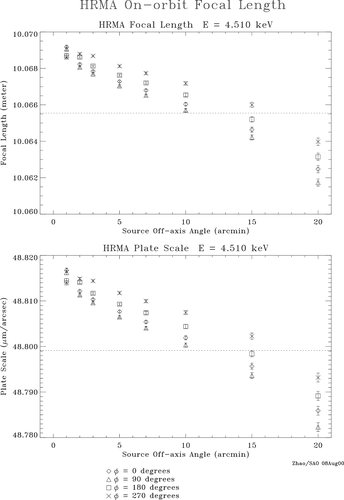
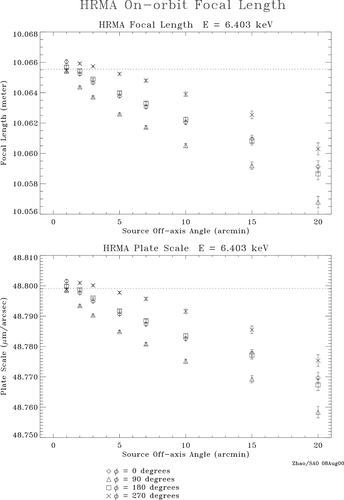
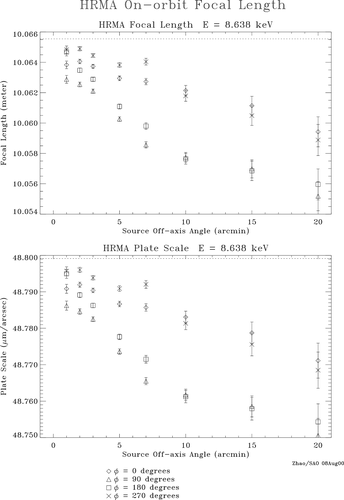
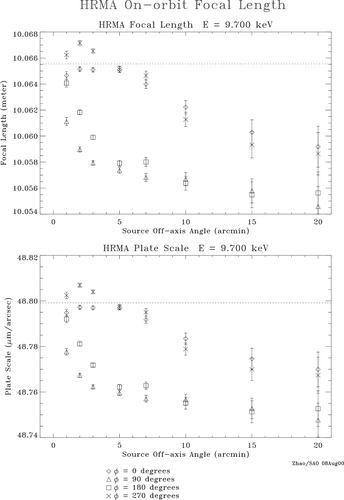
 It is seen that the HRMA FL is a function of energy and offaxis angle. And it is also slightly asymmetric azimuthally.
The following table shows the HRMA On-orbit Focal Length averaged for each energy within certain radii of offaxis angles.
It is seen that the HRMA FL is a function of energy and offaxis angle. And it is also slightly asymmetric azimuthally.
The following table shows the HRMA On-orbit Focal Length averaged for each energy within certain radii of offaxis angles.
