HRC Response to the SXRB
M. Juda
July 27, 1995
1 Introduction
The HRC instrument includes improvements over the Einstein
and ROSAT HRIs that will result in lower non-x-ray backgrounds.
The MCPs are fabricated from a ``low noise'' glass to reduce the
internally generated background.
The non-x-ray background in the ``low noise'' MCPs has been measured in
the laboratory with and without lead shielding.
Extrapolating the measurements to 100% shielding imply an internal
background of ~ 0.04 counts s-1 cm-2.
The HRC detectors will be surrounded on five sides by an active
anti-coincidence shield, signals from which will be used to
significantly reduce the cosmic ray induced background within the
data.
The on-orbit particle background incident on the detector is expected
to be 0.2 counts s-1 cm-2. The anti-coincidence shield
should permit ~ 99% of this to be identified resulting in a
residual rate of 0.002 counts s-1 cm-2.
The expected on-orbit background from all sources is ~ 0.05 counts s-1 cm-2.
The soft x-ray background (SXRB) is expected to be a significant
contributor to the observed on-orbit background but given a known
instrument response and previous observations of the SXRB, the
magnitude of its contribution can be modeled.
This memo presents estimations for the SXRB contribution to the HRC
background for both the imaging and spectroscopy detectors.
2 SXRB Intensity
There have been several surveys of the SXRB[1,2,3,4].
Among these surveys there is substantial agreement as to the SXRB
surface brightness distribution on the sky for different energy bands.
Figure 1 shows the observed spectral dependence of the
surface brightness from the UW sky survey[1] and its extension
to the 0.07-0.11 keV band[5,6].
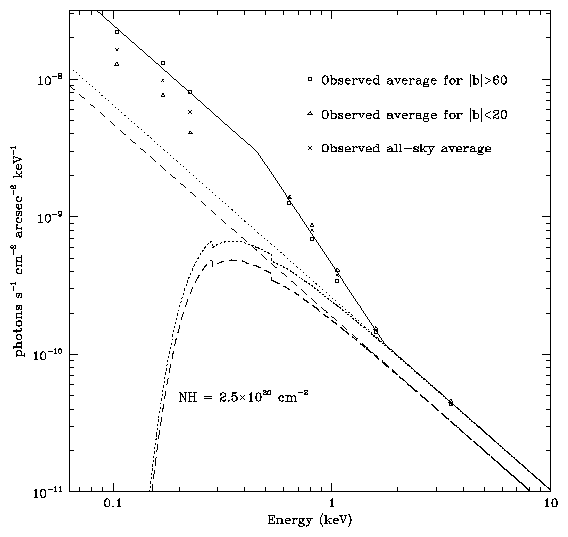
Figure 1: Observed SXRB spectrum from the UW sky survey. Different
symbols indicate the average surface brightness for different regions
of the sky. The dashed curves are for power law models of the
extragalactic background contribution with the spectrum: 8 E-1.4photons s-1 cm-2 sr-1 keV-1
for the long dashes (11 E-1.4 for
the short). The extragalactic model is plotted with and without
absorption by the neutral material in the galaxy. The HI column
density of 2.5×1020 cm-2 is typical for galactic
latitudes greater than 60°. The solid curve is an empirical fit
to the average spectrum for high galactic latitude.
Also included in the figure are models for the extragalactic
contribution to the SXRB with and without absorption. The observed
background provides a spectral shape that can be used in predictions
of the HRC response to the SXRB. The solid curve is an approximation
of the average spectrum for high galactic latitudes; this is simply
three power law segments:
|
42 E-1.4 for E < 0.457 keV |
|
|
19.2 E-2.4 for 0.457 < E < 1.745 keV |
|
and
|
11 E-1.4 for E > 1.745 keV, |
|
where the dimensions on the spectrum are photons s-1 cm-2 sr-1 keV-1.
A power law approximation is actually a poor match to the expected
spectrum below ~ 1 keV, where thermal emission from the galaxy is
expected to dominate the SXRB. It would be best to use an appropriate
line emission dominated spectrum in predicting count rates in this
energy region because the HRC energy response contains many features.
Unfortunately, the exact spectrum is not known but the calculated
rates are only slightly changed by adopting a Raymond and Smith
collisional ionization spectrum. There is also significant variation
in the SXRB at high galactic latitudes; the best count rate prediction
would be made by selecting the observed rates in the direction of the
observation.
3 Expected HRC-I Count Rate
I have used the three-segment power law approximation to predict the
average SXRB rate the HRC-I should see at high galactic latitude. The
HRC-I effective area as a function of energy function was produced
from the on-axis HRMA effective area curve, a geometric obscuration of
0.9, the transmission of the UV/ion shield with 6000 Å of
Lexan and 700 Å of aluminum[7], and the quantum
efficiency of a CsI coated MCP[8]. Figure 2
shows the spectrum multiplied by the HRC-I effective area.
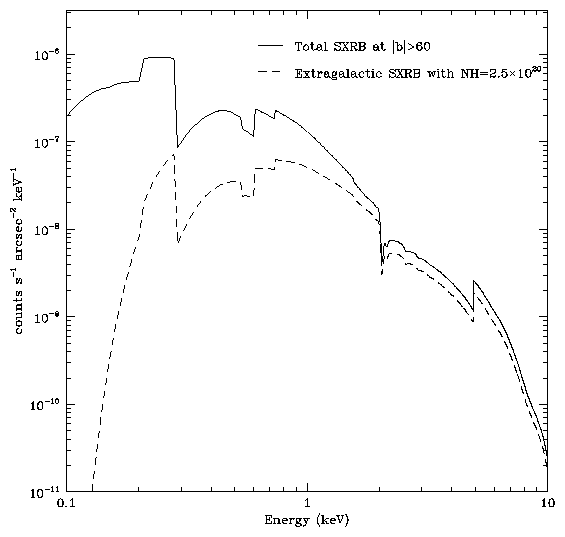
Figure 2: Product of model spectra and the HRC-I effective area. The
solid curve uses the three-segment power law spectrum that
approximates the SXRB at high galactic latitude as discussed in the
text. The dashed curve is for a model of the extragalactic
contribution: 8 E-1.4 photons s-1 cm-2 sr-1 keV-1
with absorption by a hydrogen column density of 2.5×1020 cm-2.
Also shown in the figure is the result using a model for an absorbed
extragalactic power law. Integrating these two curves over the
0.1-10.0 keV band the following HRC-I count rates are obtained: for
the average high galactic latitude spectrum, 3.04×10-7 counts s-1 arcsec-2 or 0.013 counts s-1 cm-2
and for the absorbed extragalactic component, 7.19×10-8 counts s-1 arcsec-2 or 0.0030 counts s-1 cm-2.
Unabsorbed, the extragalactic power law component produces
0.0040 counts s-1 cm-2.
Martin Zombeck performed a similar analysis using MathCAD with
slightly different results due to his assumed SXRB input spectrum.
Clearly galactic emission will dominate the observations at high
galactic latitude.
Roughly half of the rate in the high galactic latitude prediction is
from x-rays with energies less than 0.5 keV and about 85% is from
energies below 1 keV.
4 Expected HRC-S Count Rate
We can perform a similar calculation for the HRC-S.
A more interesting case may be that for the background in the low
energy portion of the dispersed LETG spectrum.
As a specific example, I consider here the contribution from the SXRB
at 30 arcmin in the dispersion direction.
This location corresponds to ~ 87 Å or 0.143 keV in the
LETGS first order.
The zero order image of the SXRB 30 arcmin off-axis will appear as a
background to the dispersed spectrum.
The HRMA effective area at 30 arcmin off axis has been tabulated and
can be found in /afs/cfa/axaf/cal_db/HRMA/area/axaf_eval.out.
The UV/ion shield over this part of the HRC-S has 2500 Å
Lexan and 300 Å aluminum.
I assume a CsI photocathode, rather than KBr, in line with the HRC PIs
current plans.
The LETG introduces an additional geometric obscuration factor of 0.7.
The zero order diffraction efficiency of the LETG is ~ 0.25 but
depends somewhat on energy.
Diffracted SXRB x-rays from other off-axis angles will also contribute
to the background at this location on the detector.
The LETG first order diffraction efficiency must be combined with the
HRMA area appropriate for the energy-dependent, off-axis angle.
For a given energy, the two off-axis angles that contribute first order
diffracted photons are calculated then the HRMA effective area
determined.
In finding the effective HRMA area at these angles, I have approximated
the vignetting as
where A
is the area and f is the off-axis angle measured in arcmin, this
functional form crudely describes the behavior for energies less than
~ 1 keV (note: this was done only for calculating the contribution
of diffracted x-rays not the zero order).
Integrating the average high galactic latitude background spectrum
over the interval 0.05-10.0 keV results in a rate of
1.09×10-7 counts s-1 arcsec-2 or 0.0046 counts s-1 cm-2.
5 Concluding Remarks
The ASC data system has a requirement to generate models for various
background components including that of the sky background.
The SXRB will generate a significant, if not dominant, component of the
on-orbit background of the HRC; however,
the magnitude of this contribution is calculable based on the
known response of the HRC-I and HRC-S detectors and previous
measurement of the surface brightness of the SXRB.
The instrument response will be measured during the currently planned
calibrations, with the possible exception of the response of the LETGS
(HRMA/LETG/HRC-S) to x-rays from large ( > 30 arcmin) off-axis angles.
Maps of the SXRB from the data of the ROSAT sky
survey[4] provide the most detailed information on the
spatial structure of the SXRB below 2 keV. In the next version of these
maps it is planned to provide information on finer spatial scales and
narrower pulse-height bands.
The broad-band spectral behavior of the SXRB below 0.3 keV is
currently best characterized by data from the Wisconsin sky
survey[1].
The ASC should acquire the best available data on which to base
predictions for the SXRB contribution to individual observations.
References
- [1]
- D. McCammon et al. 1983, ApJ, 269, 107.
- [2]
- F. Marshall & G. Clark 1984, ApJ, 287, 663.
- [3]
- G. P. Garmire et al. 1992, ApJ, 399, 694.
- [4]
- S. L. Snowden et al. 1995, ApJ, submitted.
- [5]
- J. J. Bloch et al. 1986, ApJL, 308, L59.
- [6]
- M. Juda et al. 1991, ApJ, 367, 182.
- [7]
- M. Juda, Memo to ASC dated 1994 September 9, ``HRC
UV/Ion Shields''
- [8]
- M. V. Zombeck, 1995, Mathcad document
HRCMODEL.MCD
Dr. Michael Juda
Harvard-Smithsonian Center for Astrophysics
60 Garden Street, Mail Stop 70
Cambridge, MA 02138, USA
Ph.: (617) 495-7062
Fax: (617) 495-7356
E-mail: mjuda@cfa.harvard.edu
File translated from TEX by TTH, version 2.01.
On 11 Mar 1999, 11:31.


